Le Mappe di Karnaugh.
Le mappe di Karnaugh rappresentano un metodo grafico-sistematico
per la semplificazione di qualsiasi funzione booleana. Questo metodo si basa
su poche regole e se applicate tutte contemporaneamente portano sempre alla
massima semplificazione delle espressioni booleane.
Una mappa di Karnaugh (mappa di K) è costituita da una serie di celle adiacenti
opportunamente disposte. Ogni cella rappresenta una particolare combinazione
delle variabili d'entrata, che compaiono nell'espressione booleana, sotto forma
di prodotto (se si considerano i MinTermini).
Se n sono le variabili d'entrata della rete, la mappa di K. prevede
2n celle, perché 2n sono le combinazioni
possibili di n variabili booleane. Un'espressione con due variabili A e B richiede
una mappa di K con 4 celle, come mostrato in figura:
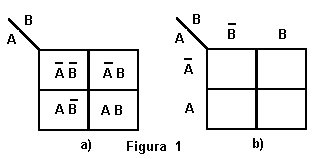
Nella mappa di figura a), sono mostrate le quattro celle contenenti tutte le
possibili combinazioni tra due variabili binarie A e B; la figura b), invece,
mostra come viene disegnata la mappa di K, per il suo impiego nella semplificazione
delle funzioni booleane: le variabili sono poste esternamente alle celle. Si
noti come le celle siano collocate in modo tale che qualsiasi coppia di celle
vicine (adiacenti) si consideri, cambi di stato una sola variabile. Altre forme
di mappe di K per tre e quattro variabili:
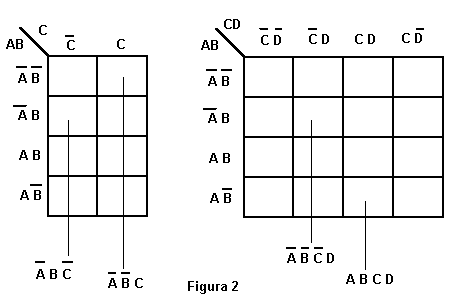
Celle Adiacenti
Si definiscono celle adiacenti due celle che rappresentano due
combinazioni per le quali cambia di stato una sola variabile. In genere sono
adiacenti tutte le celle che hanno un lato in comune, quelle agli estremi delle
righe e quelle agli estremi delle colonne.
Mappa di Karnaugh e espressioni
booleane
Per conoscere il comportamento di una rete logica si determina la tavola della
verità e da questa si risale alla funzione logica espressa come una delle due
forme canoniche: SOP cioè somma di prodotti (MinTermini) o POS
cioè come prodotti di somme (MaxTermini).
Per rappresentare una funzione booleana con la mappa di K, considerandola sottoforma
di somma di prodotti, per ogni termine prodotto (MinTermine) si scrive un 1
nella cella corrispondente della mappa di K.
Ad esempio:
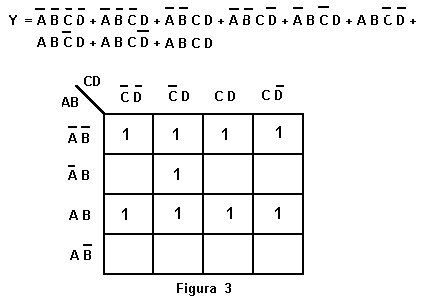
In altre parole la mappa di K non è altro che un modo diverso di rappresentare
la tavola della verità della funzione logica data.
La mappa di Karnaugh e la semplificazione di
una funzione logica.
Si devono creare gruppi o raggruppamenti di
1 che si trovano in celle adiacenti seguendo le seguenti regole:
1) I raggruppamenti si effettuano per insiemi di celle in numero pari ad una
potenza del 2: 1,2,4,8,16... .
2) I raggruppamenti devono comprendere il maggior numero di celle
possibili nel rispetto della regola 1). Una o più celle possono appartenere a
più raggruppamenti.
3) I raggruppamenti devono ricoprire tutte le celle contenenti un 1; in
altre parole ogni cella con un 1 deve far parte di un raggruppamento, che al
limite può essere costituito da una sola cella.
4) Ad ogni raggruppamento corrisponde un prodotto delle variabili d'entrata
così strutturato: il prodotto comprende solo quelle variabili che nel raggruppamento
in esame non cambiano di stato, complementando quelle che sono allo stato 0.
La funzione logica semplificata è data dalla somma di questi prodotti
generati dai raggruppamenti.
Applicando le regole viste all'esempio di Figura 3,
si ottiene:
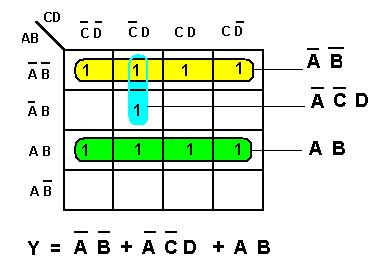
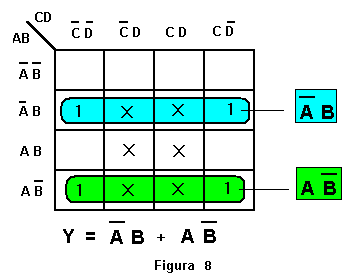
Esercizio 1
Si noti, in questo esempio come uno dei due raggruppamenti sia realizzato con
i quattro 1 posti nelle celle d'angolo della mappa di K.
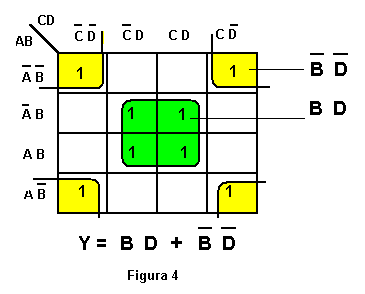
Esercizio 2
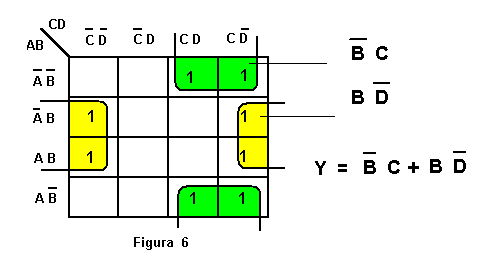
Esercizio 3
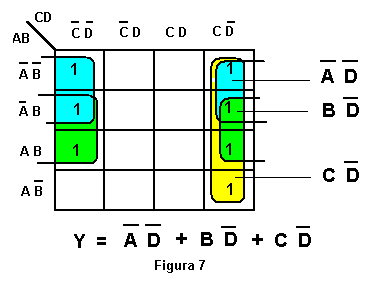
Le condizioni di
indifferenza
Nel progetto di reti logiche, a volte, si presentano combinazioni
delle variabili d'entrata non permesse. Ad esempio il codice BDC (Binary Deimal
Code) codifica solo le 10 cifre decimalie e servono 4 bit per la loro codifica.
Le possibili combinazione con 4 bit sono 16, nel caso del codice BCD ne servono
10, da 0000,... fino a 1001; le altre 6, a partire da 1010, ... fino a 1111
non sono ammesse. Dovendo costruire una macchina logica con 4 variabili d'entrata
che operi soltanto su numeri in BCD è ovvio che le 6 combinazioni suddette non
sono codici BCD validi, ma possibili. Queste combinazioni possono essere considerate
di indifferenza, nel senso che non avverranno mai.
L'importanza delle condizioni di indifferenza si manifesta nella semplificazione
delle mappe di Karnaugh, perchè ognuna di esse può indifferentemente
assumere il valore 0 oppure 1 senza influenzare il funzionamento della
macchina logica. In questo modo, aumentando il numero degli 1 presenti nella
mappa, aumenta la semplificazione dell'espressione della funzione logica e di
conseguenza si ottimizza anche il numero di porte per realizzare
il circuito.
Nella mappa di
Karnaugh le condizioni di indifferenza vengono indicate con una X.
Si
consideri l'esempio di figura: